引自Fabian Suchanek的讲义。
总结:如何扩张KB并且使KB打到最大权重即MAXSAT,可以使用穷举法或者Unit Propagation方法,各有利弊。要知道如何使用在有命名的corpus上对实例做标记,例如@D42,利用occurs,means,R等进行pattern detection和pattern application以及消除过程中二义性等问题的方法。
在进行信息提取的时候,我们经常会遇到的问题,再上一个章节已经提到:
例如:
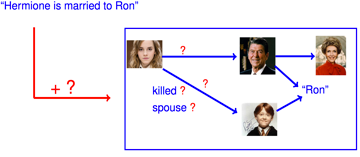
即二义性的问题,图中hermione和ron结婚但是有两个人都有ron的标签,我们无法判断到底她和谁结了婚。
需要知道的一些定义:
atom:命题陈述Propositional statement
polarity:positive,negative,在KB中positive永远为正,KB中永远不会出现negative,若KB中既无某原子的正也没有负,说明负是正确的。
Conjunction:且
Disjunction:或,可以被写成Clause,例如{A , B} 相当于A or B
Implication:A-->B, 相当于nonA or B
通用量化公式universally quantified formula:相关实例的简写符号 shorthand of related instances 例如:hasSpouse(X,Y) -> has(Y,X) 是 hasSpouse(aa,bb) -> has(bb,aa),hasSpouse(cc,dd) -> has(dd,cc),etc的简写
加权规则weighted rules:带有weight的rules
KB的权重:KB中所有rules的权重之和
MAX SAT:找到KB的最高权重的过程,若有多种情况可使KB打到最大权重,则看哪种情况使用的原子数目少,则哪种更好
MAX SAT的方法:
1穷举法Exhausted search
列出KB中所有rules的atoms,进行排列组合,尽可能使KB的的权重最大
有点:正确,完整 缺点:复杂度超高,有2的n次方个可能世界
2 单位传播Unit Propagation
针对rules的情况:
- 把单个的rules添加至KB,我们简称它为a
- 把其他rules中的a都删掉
- 若一条rules都被满足,则把此rules删掉
针对clauses的情况:
- 删掉单个的atom,我们简称为a
- 把其他clause中的a删掉
- 把其他clause中a的否定删掉
优点:正确 缺点:不完整,因为只有当一个atom比它的否定相关的所有rules的权重之和大是才可进行传播
小练习:进行unit propagation
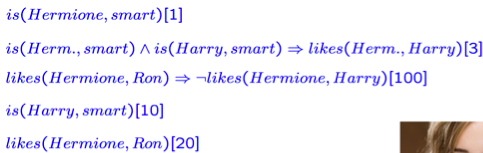
尽可能找权重高的单独的atom,我选择likes(Hermione, Ron) ,但是它的权值比它的否定相关的rules总和小,化简第三条rules,否定的权值为100,所以不propagation,重复此过程,最终最高权重KB为:
is(Harry,Smart)[10], is(Hermione,smart), likes(Hermione,Harry)[3] 总权重为111即1,3,4 成立
使MAX SAT得到更好的结果的方法:
@font-face { font-family: "Cambria Math"; }@font-face { font-family: "DengXian"; }@font-face { font-family: "@DengXian"; }p.MsoNormal, li.MsoNormal, div.MsoNormal { margin: 0cm 0cm 0.0001pt; font-size: 12pt; font-family: "Times New Roman"; }.MsoChpDefault { font-family: DengXian; }div.WordSection1 { }
例如:原子数少时进行穷举,尽可能先找权重大的atoms或者使权重大的rules成立,etc
一致性:在rules当中添加类似于different,means,type等relation确保一致性
例如:hasSpouse(X ,Y) and different(Y,Z) => non hasSpouse(X,Z)
KB可以用rules来表达
例如:KB中有一个原子,张这样:A(X,Y)[100]
写成rules - A(X,Y) [100]
假设完整:为了使KB更完整,我们可在KB中添加rules的例子
例如:non A(X,Y)[100] , 我们添加non A(aaa,bbb) [100] , non A(ccc,ddd) [100]
把corpus写成rules:主要用到了occurs,means,different
例如:我们有一个corpus叫D42,内容为:Hermione married Ron
Occurs(Hemione@D42,married,Ron@D42):此处的D42就是表示我们文章中的
但同一篇文章中容易个Ron也有可能有多个含义,此时用mean表示,例如:
means(D42, Ronauld)
means(D42,RonWeasly)
为了消除这种二义性,我们可以用context消歧或者prior消歧
例如:Occurs(Hemione@D42,married,Ron@D42) [3] 后面的3代表了3次
means(D42, Ronauld) [5]
means(D42,RonWeasly) [7]
means 后面的数字是根据Disambiguation来的,重叠次数
means(X,Y) and different(Y,Z) => non means(X,Z) 这种rules属于很hard的rule,需要高权重
我们再上一张讲过parttern推理的方法,现在在我们用occurs,means,R来进行parttern推理,最后得到isPartternfor的结果:
例如:KB : Reagon—hasSpouse -->Davis
corpus : Reagon married to Davis
根据上一章节讲的parttern推理方法,可以知道married(X,Y) 是hasSpouse(X,Y)的一个pattern,若我们用occurs,means,R该如何推理呢?
从KB中可得:hasSpouse(Reagon, Davis)
occurs(R@1,married,D@1) 假设我们的corpus叫1
means(R@1, Reagon)
means(D@1, Davis)
=> occurs(X,P,Y) and means(X,X’) and means(Y,Y’) and R(X’,Y’) => isPatternFor(P,R)
所以此时isPatternFor(married, hasSpouse)
运用pattern,是推理Pattern的反过程,即·
occurs(X,P,Y) and means(X,X’) and means(Y,Y’) and isPatternFor(P,R) => R(X’,Y’)
小练习:运用Pattern推理和Pattern应用,每条rules的权重为1,找到最好的world

用1,2,3,4运用Pattern deduction,即:
occurs(P@1, « adores », E@1) and means(E@1, Elvis) and means(P@1, Priscilla) and hasSpouse(Priscilla, Elvis) => isPatternFor(adores, hasSpouse) 我们简称7式
用5672进行Pattern applying,即
occurs(M@1, « adores »,E@1) and means(M@1, Madonna) and means(E@1, Elvis) and isPatternFor(adores, hasSpouse) => hasSpouse(Madonna,Elvis)
会遇到的问题:二义性,corpus本身有问题,解析句子出现问题,出现矛盾例如接了两次婚
例如:
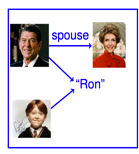
我们不知道到底是哪个ron和Davis结了婚
如何解决这些问题:找到最可信的world
利用关系的对称性:hasSpouse(X,Y) => hasSpouse(Y,X)
- 从pattern推理得到的rules进行实践的时候权重要小
- 从KB中直接拿来用的 rules权重要高